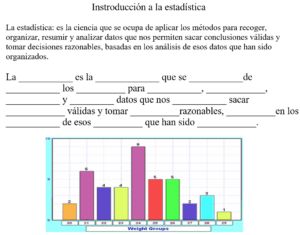
Introducción a la estadistíca:






Respuestas del ejercicio anterior.
1) 5x = 17 x 20 de donde x = 17 x 20 /5 entonces x = 68
2) 15x = 6 x 20 de donde x = 6 x 20/15 entonces x = 8
3) 12x = 9 x 16 de donde x = 9 x 16/12 entonces x = 12
4) 8x = 4 x 16 de donde x = 4 x 16/8 entonces x = 8
5) 96x = 12 x 40 de donde x = 12 x 40/96 entonces x = 5
6) 32x = 8 x 48 de donde x = 8 x 48/32 entonces x = 12
7) 5x = 45 x 10 de donde x = 45 x 10/5 entonces x = 90
8) 8x = 16 x 25 de donde x = 16 x 25/8 entonces x = 50
9) 20x = 38 x 44 de donde x = 38 x 44/20 entonces x = 83.6
10) 78x = 88 x 30 de donde x = 88 x 30 /78 entonces x = 33.84


Respuestas del ejercicio anterior.
1) x = 4 x 6 donde x = 24
2) 10x = 60 x 6 donde x = 60 x 6 /10 entonces x = 36
3) 6x = 4 x 42 donde x = 4 x 42 /6 entonces x = 28
4) 12x = 16 x 9 donde x = 16 x 9 /12 entonces x = 12
5) 15x = 12 x 45 donde x = 12 x 45 /15 entonces x = 36



Respuestas del ejercicio anteror.
1) 1/2x = 3 x 4 de donde x = 3 x 4/1/2 entonces x = 24
2) 3x = 12 x 3/4 de donde x = 12 x 3/4/3 entonces x =3
3) 2/3x = 8 x 9 de donde x = 8 x 9/2/3 entonces x = 108
4) 1/5x = 3/4 x 4/5 de donde x = 3/4 x 4/5 /1/5 entonces x = 3
5) 1/2x = 3/5 x 5 de donde x = 3/5 x 5 /1/2 entonces x = 6
6) 15x = 3/5 x 10 de donde x = 3/5 x 10 /15 entonces x = 2/5
7) 3/4x = 6 x 2/3 donde x = 6 x 2/3 /3/5 entonces x = 5 1/3
8) 20x = 0.5 x 30 donde x = 0.5 x 30 /20 entonces x = 3/4
9) 0.6x = 0.4 x 40 donde x = 0.4 x 40 /0.6 entonces x = 26.66
10) 18x = 2 /5 x 1 /6 donde x = 2 /5 x 1 /6 /18 entonces x = 1 /270




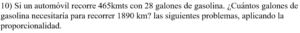
Respuestas del ejercicio anterior.
1) En este problema, aplicamos la proporcionalidad para resolverlo, donde cada parte va con su parte, o sea, 175 / 1385 = 13 / x luego, 175x = 1385 x 13 entonces x = 1385 x 13 / 175 por lo que x = 102.88 libras.
2) 1) En este problema, aplicamos la proporcionalidad para resolverlo, donde cada parte va con su parte, o sea, 2 /x = 1 /12.5 luego x = 2 x 12.5 por lo que x = 25 pulgadas de nieves.
3) 1) En este problema, aplicamos la proporcionalidad para resolverlo, donde cada parte va con su parte, o sea, 878 /x = 1 /3meses, pero los tres meses hay que llevarlos a días, que son 90 días, luego, x = 878 x 90 por lo que x = 79,020 camisas.
4) En este problema, aplicamos la proporcionalidad para resolverlo, donde cada parte va con su parte, o sea, 18 /180 = 7 /x luego 18x = 180 x 7 entonces x = 180 x 7 /18 por lo que x = 70 horas
5) En este problema, aplicamos la proporcionalidad para resolverlo, donde cada parte va con su parte, o sea, 90 /x = 2 /25 luego 2x = 90 x 25 entonces x = 90 x 25 /2 por lo que x = 1125 que son las piezas que produce un solo trabajador, ahora multiplicamos ese producto por 7, 125 x 7 = 7,875 piezas producen los 7 trabajadores.
6) En este problema, aplicamos la proporcionalidad para resolverlo, donde cada parte va con su parte, o sea, 8 /36 = 12 /x luego 8x = 36 x 12 entonces x = 36 x 12 / 8 por lo que x = 54 metros de altura.
7) En este problema, aplicamos la proporcionalidad para resolverlo, donde cada parte va con su parte, o sea, 5 / x = 47 / 160 luego 47x = 5 x 160 entonces x = 5 x 160 / 47 por lo que x = 17 pulgadas.
8) En este problema, debemos convertir los 5 años a semanas multiplicando 5 x 52 = 260 semanas, luego, multiplicamos 260 x 480 = $124,800 en los 5 años.
9) En este problema, debemos convertir la hora en segundo, multiplicando 60 x 60 = 3600 segundos y luego, aplicamos la proporcionalidad para resolverlo, o sea, 12 /x = 1 / 3600 luego x = 12 3600 por lo que x = 43,200 frezas, que es la cantidad que recoge el primer hombre. El segundo hombre recoge 20 / x = 1 / 3600 luego x = 20 x 3600 por lo que x = 72,000 frezas. Ahora, establecemos la diferencia entre 72000 – 43200 = 28,800 frezas, recoge más que el otro hombre.
10) En este problema, aplicamos la proporcionalidad para resolverlo, donde cada parte va con su parte, o sea, 465 / 1890 = 28 /x luego 465x = 28 x 1890 entonces x = 28 x 1890 / 465 por lo que x = 113.80 galones.

