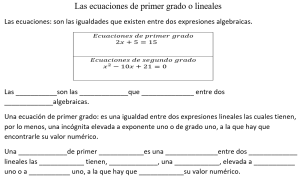
Ecuaciones de primer grado o lineales.
ALGEBRA




ALGEBRA

Resuelve las siguientes ecuaciones de primer grado.
Respuestas del ejercicio anterior.
1) x + 3 = 8 entonces x = 8 – 3 luego x = 5
2) y – 1.5 = 3.2 entonces y = 3.2 + 1.5 luego y = 4.7
3) 12. 5 = y + 7.75 organizamos la ecuación y + 7.75 = 12.5 entonces y = 12.5 – 7.75 luego y = 4.75
4) 24 = d + 15.2 organizamos la ecuación d + 15.2 = 24 entonces d = 24 – 15.2 luego d = 8.8
5) y – 5 / 8 = 1 / 4 entonces y = 1/4 + 5/8 luego sumamos las fracciones
y = 1x2 / 4x2 + 5/ 8 donde y = 2 / 8 + 5 / 8 por lo que y = 7 /8
6) x + 4/7 = 2/3 entonces x = 2 / 3 – 4/7 luego restamos las fracciones
x = 2 / 3 – 4 / 7 donde x = 14 – 12 /21 por lo que y = 2 / 21
7) y + 3/8 = 4/7 entonces y = 4 / 7 – 3 /8 luego restamos las fracciones
y = 4 / 7 – 3/ 8 donde y = 32 – 21 / 56 por lo que y = 11 / 56
8) 8.6 = x – 5. 475 organizamos la ecuación x – 5.475 = 8.6 entonces x = 8.6 + 5.475 luego x = 14.075
9) 2/9 = y – 4/5 organizamos la ecuación y – 4 /5 = 2 / 9 entonces y = 2 / 9 + 4 / 5 luego sumamos las fracciones y = 10 + 36 / 45 donde y = 46 / 45 simplificando y = 1 1 /45
10) x + 5/11 = 2/5 entonces x = 2 / 5 – 5 /11 luego restamos las fracciones
x = 2 / 5 – 5 / 11 donde y = 22 – 25 / 55 por lo que y = -3 / 55
ALGEBRA


Respuestas del ejercicio anterior.
1) 5 x = 20 como el 5 esta multiplicando, entonces, pasa dividiendo, o sea, x = 20 /5 luego x = 4
2) 3 y = 3 como el 3 esta multiplicando, entonces, pasa dividiendo, o sea, y = 3 /3 luego x = 1
3) 3 x = 15 como el 3 esta multiplicando, entonces, pasa dividiendo, o sea, x = 15 /3 luego x = 5
4) 10 c = 90 como el 10 esta multiplicando, entonces, pasa dividiendo, o sea, c = 90 /10 luego c = 10
5) 7 y = 84 como el 7 esta multiplicando, entonces, pasa dividiendo, o sea, y = 84 /7 luego y = 12
6) 5 x = 100 como el 5 esta multiplicando, entonces, pasa dividiendo, o sea, x = 100 /5 luego x = 20
7) 20 r = 200 como el 20 esta multiplicando, entonces, pasa dividiendo, o sea, r = 200 /5 luego x = 40
8) 15 s = 75 como el 15 esta multiplicando, entonces, pasa dividiendo, o sea, s = 75 /15 luego x = 5
9) 25 x = 1000 como el 25 esta multiplicando, entonces, pasa dividiendo, o sea, x = 1000 /25 luego x = 40
10) 50 z = 50 como el 50 esta multiplicando, entonces, pasa dividiendo, o sea, z = 50 /50 luego x = 1
ALGEBRA



Respuestas del ejercicio anterior.
1) x / 3 = 10 como el 3 esta dividiendo, entonces, pasa multiplicando, o sea, z = 10 x 3 luego x = 30
2) y / 20 = 100 como el 20 esta dividiendo, entonces, pasa multiplicando, o sea, y = 100 x 20 luego y = 2000
3) s / 10 = 200 como el 10 esta dividiendo, entonces, pasa multiplicando, o sea, s = 200 x 10 luego s = 2000
4) z / 7 = 80 como el 7 esta dividiendo, entonces, pasa multiplicando, o sea, z = 80 x 7 luego z = 560
5) r / 60 = 12 como el 60 esta dividiendo, entonces, pasa multiplicando, o sea, r = 12 x 60 luego r = 720
6) x / 30 = 20 como el 30 esta dividiendo, entonces, pasa multiplicando, o sea, z = 20 x 30 luego z = 600
7) y / 12 = 60 como el 12 esta dividiendo, entonces, pasa multiplicando, o sea, y = 60 x 12 luego y = 720
8) m / 21 = 90 como el 21 esta dividiendo, entonces, pasa multiplicando, o sea, m = 90 x 21 luego m = 1890
9) n / 38 = 1200 como el 38 esta dividiendo, entonces, pasa multiplicando, o sea, n = 1200 x 38 luego n = 45,600
10) x / 8 = 120 como el 8 esta dividiendo, entonces, pasa multiplicando, o sea, x = 120 x 8 luego x = 960
ALGEBRA

ALGEBRA




Respuestas del ejercicio anterior.
Resuelve las siguientes ecuaciones de primer grado.
1) 5 b – 3 = 32 en este caso aplicamos las operaciones inversas 3b = 32 + 3 de donde 5b = 35 entonces 5b = 35 luego b = 35/5, por lo tanto, b = 7
2) 7 x – 2 = 1 en este caso aplicamos las operaciones inversas 7x = 1 + 2 de donde 7x = 3 entonces x = 3 / 7
3) n / 6 + 4 = 22 en este caso aplicamos las operaciones inversas n / 6 = 22 – 4 de donde n = 18 x 6 entonces n = 108
4) 2 x / 14 + 5 = 25 en este caso aplicamos las operaciones inversas 2x / 4 = 25 – 5 de donde 2x = 20 x 14 entonces 2x = 280 luego x = 280 / 2, por lo tanto, x = 140
5) 9 y / 3 – 7 = 57 en este caso aplicamos las operaciones inversas 9y / 3 = 57 + 7 de donde 9y = 54 x 3 entonces 9y = 162 luego y = 162 / 9, por lo tanto, y = 18
6) 4 t / 2 + 8 = 80 en este caso aplicamos las operaciones inversas 4t / 2 = 80 – 8 de donde 4t = 72 x 2 entonces 4t = 144 luego t = 144 / 4, por lo tanto, t = 36
7) 5 r / 6 – 20 = 90 en este caso aplicamos las operaciones inversas 5r / 6 = 90 + 20 de donde 5r = 110 x 6 entonces 5r = 660 luego r = 660 / 5, por lo tanto, r = 132
8) 39 = 5 x / 2 en este caso organizamos la ecuación y luego aplicamos las operaciones inversas 5x / 2 = 39 de donde 5x = 39 x 2 entonces 5x = 78 luego x = 78 / 5, por lo tanto, x = 15.6
9) 46 = 7 y / 5 en este caso organizamos la ecuación y luego aplicamos las operaciones inversas 7y / 5 = 46 de donde 7y = 46 x 5 entonces 7y = 230 luego y = 230 / 7, por lo tanto, x = 32.85
10) 120 = 3 z / 5 en este caso organizamos la ecuación y luego aplicamos las operaciones inversas 3z / 5 = 120 de donde 3z = 120 x 5 entonces 3z = 600 luego z = 600 / 3, por lo tanto, z = 200
ALGEBRA


Respuestas del ejercicio anterior.
1) x – 7 / 3 = 65 en este caso aplicamos las operaciones inversas x – 7 = 65 x 3 de donde x – 7 = 195 entonces x = 195 + 7 luego x = 202
2) 5 x + 30 / 4 = 80 en este caso aplicamos las operaciones inversas 5x + 30 = 80 x 4 de donde 5x = 320 – 30 entonces 5x = 290 luegox = 290 / 5, por lo tanto, x = 58
3) 6 y – 12 / 2 = 45 en este caso aplicamos las operaciones inversas 6y – 12 = 45 x 2 de donde 6y = 90 + 12 entonces y = 102 / 6 luego x = 17
4) 2 n + 9 / 6 = 100 en este caso aplicamos las operaciones inversas 2n + 9 = 100 x 6 de donde 2n = 600 – 9 entonces n = 591/2 luego n = 295.5
5) 4 w – 11 / 3 = 30 en este caso aplicamos las operaciones inversas 4w – 11 = 30 x 3 de donde 4w = 90 + 11 entonces w = 101 / 4 luego w = 25.25
6) 3x – 10 /4 = 25 en este caso aplicamos las operaciones inversas 3x – 100 = 25 x 4 de donde 3x = 100 + 10 entonces x = 110 /3 luego x = 36.66
7) 3x/5 + 16 = 24 en este caso aplicamos las operaciones inversas 3x / 5 = 24 – 16 de donde 3x = 8 x 5 entonces x = 40 / 3 luego x = 13.33
8) 6x /7 – 15 = 18 en este caso aplicamos las operaciones inversas 6x / 7 = 18 + 15de donde 6x = 33 x 7 entonces x = 331 / 6 luego x = 38.5
9) 8x/3 – 20 = 50 en este caso aplicamos las operaciones inversas 8x / 3 = 50 + 20 de donde 8x = 70 x 3 entonces x = 210 / 8 luego x = 26.25
10) 10x – 12 /5 = 100 en este caso aplicamos las operaciones inversas 10x – 12 = 100 x 5 de donde 10x = 500 + 12 entonces x = 512 / 10 luego x = 51.2



Respuestas del ejercicio anterior.
Resolver ecuaciones de la forma literal.
1) 5 x – 9 = 3 x + 27 entonces 5x – 3x = 27 + 9 de donde 2x = 36,luego x = 36/2, por lo tanto, x = 18
2) 2x – 14 = x + 6 entonces 2x – x = 6 + 14 dedonde x = 20
3) 2x/5 = 60 entonces 2x = 60 x 5 de donde x = 300/2, por lo tanto, x = 150
4) 3x/4 + 7 = 31 entonces 3x/4 = 31 – 7 de donde 3x = 24 x 4, luego x = 96/3, por lo tanto, x = 32
5) En éste problema, aplicamos la proporcionalidad, por lo que, tenemos que expresar cada parte con su parte. Entonces , debemos colocar sombra con sombra y altura con altura, osea, 6/x = 3/24 de donde x = 6 x 24/3, por lo tanto, x = 48 pies
6) 2( x + 7) = x + 20 entonces 2x + 14 = x + 20 de donde 2x – x = 20 – 14, por lo tanto, x = 6
7) En éste problema, aplicamos la proporcionalidad, por lo que , tenemos que expresar cada parte con su parte. Entonces, debemos colocar kilomertos con kilimetros y galones con galones, osea, 360/900 = 20/x de donde x = 900 x 20/360, luego x = 18,000/360, por lo tanto,x = 50 galones.
8) x + 2x = 96 entonces 3x = 96 de donde x = 96/3, luego x = 32, por lo tanto, los golfistas aficionados son el doble, osea 2(32) = 64.
9) x / 12 = 6 entonces x = 6 x 12 donde x = 72
10) x – 5 = 14 entonces x = 14 + 5 donde x = 19



Respuestas del ejercicio anterior.
Resuelve las siguientes ecuaciones de primer grado.
1) 2 (7 x – 5) + 7 = 25 en ste caso resolvemos las operaciones indicada y luego aplicamos las operaciones inversas, o sea, multiplicamos el 2 por cada uno de los términos que están dentro del parentecis, por lo que, 14x – 10 + 7 = 25 ahora, podemos aplicar las operaciones inversas, 14x = 25 + 10 – 7 donde 14x = 28 entonces x = 28 / 14 por lo tanto, x = 2
2) 5 (d + 3) – 10 = 15 en ste caso resolvemos las operaciones indicada y luego aplicamos las operaciones inversas, o sea, multiplicamos el 5 por cada uno de los términos que están dentro del parentecis, por lo que, 5d + 15 – 10 = 15 ahora, podemos aplicar las operaciones inversas, 5d = 15 – 15 + 10 donde 5d = 10 entonces d = 10 / 5 por lo tanto, d = 2
3) 4 (6 b – 3) / 2 + 8 = 32 en ste caso resolvemos las operaciones indicada y luego aplicamos las operaciones inversas, o sea, multiplicamos el 4 por cada uno de los términos que están dentro del parentecis, por lo que, 24b – 12 / 2 + 8 = 32 ahora, podemos aplicar las operaciones inversas, 24b – 12 / 2 = 32 – 8 donde 24b – 12 = 24 x 2 entonces 24b = 48 + 12 luego b = 60 / 24 por lo tanto, b = 2.5
4) 10 (x + 5) / 4 – 20 = 95 en ste caso resolvemos las operaciones indicada y luego aplicamos las operaciones inversas, o sea, multiplicamos el 10 por cada uno de los términos que están dentro del parentecis, por lo que, 10x + 50 / 4 – 20 = 95 ahora, podemos aplicar las operaciones inversas, 10x + 50 / 4 = 95 + 20 donde 10x + 50 = 115 x 4 entonces 10x = 460 – 50 luego x = 410 / 10 por lo tanto, b = 41
5) 3 (2 x – 8) – 9 / 4 = 34 en ste caso resolvemos las operaciones indicada y luego aplicamos las operaciones inversas, o sea, multiplicamos el 3 por cada uno de los términos que están dentro del parentecis, por lo que, 6x – 24 – 9 / 4 = 34 ahora, podemos aplicar las operaciones inversas, 6x – 24 – 9 = 34 x 4 donde 6x = 136 + 24 + 9 entonces 6x = 169 luego x = 169 / 6 por lo tanto, x = 28.16
6) 10y – (5y + 8) = 42 en ste caso resolvemos las operaciones indicada y luego aplicamos las operaciones inversas, o sea, multiplicamos el (- ) por cada uno de los términos que están dentro del parentecis, por lo que, 10y – 5y – 8 = 42 ahora, podemos reducir los términos semejantes, 5y – 8 = 42 aplicamos las operaciones inversas, 5y = 42 + 8 entonces y = 50 / 5 por lo que, y = 10
7) 4(x – 6) /3 = 30 en ste caso resolvemos las operaciones indicada y luego aplicamos las operaciones inversas, o sea, multiplicamos el 4 por cada uno de los términos que están dentro del parentecis, por lo que, 4x – 24 / 3 = 30 ahora, podemos aplicar las operaciones inversas, 4x – 24 = 30 x 3 donde 4x = 90 + 24 entonces x = 114 / 4 por lo tanto, x = 28.5
8) 3(2y + 1) – 7 = 50 en ste caso resolvemos las operaciones indicada y luego aplicamos las operaciones inversas, o sea, multiplicamos el 3 por cada uno de los términos que están dentro del parentecis, por lo que, 6y + 3 – 7 = 50 ahora, podemos aplicar las operaciones inversas, 6y = 50 – 3 + 7 donde 6y = 54 entonces y = 56 / 6 por lo tanto, y = 9.33
9) 15y – 2(y + 6) = 14 en ste caso resolvemos las operaciones indicada que están afectadas por el signo (-) y luego aplicamos las operaciones inversas, o sea, multiplicamos el (-2) por cada uno de los términos que están dentro del parentecis, por lo que, 15y – 2y – 12 = 14 ahora, reducimos los términos semejantes 13y – 12 = 14, despues, podemos aplicar las operaciones inversas, donde 13y = 14 + 12 entonces y = 26 / 13 por lo tanto, y = 2
10) 28x – 6 (3x – 5) = 40 en ste caso resolvemos las operaciones indicada que están afectadas por el signo (-) y luego aplicamos las operaciones inversas, o sea, multiplicamos el (-6) por cada uno de los términos que están dentro del parentecis, por lo que, 28x – 18x + 30 = 40 ahora, reducimos los términos semejantes 10x + 30 = 40, despues, podemos aplicar las operaciones inversas, donde 10x = 40 – 30 entonces y = 10 / 10 por lo tanto, y =1



Respuestas del ejercicio anterior.
Resolver ecuaciones de primer grado con signos.
1) x+ 9 = 4 entonces x = 4 – 9 de donde x = – 5
2) w – 25 = 6 entonces w = 6 + 25 de donde w = 19
3) k – 10 = 28 entonces k = 28 + 10 de donde k = 18
4) m + 26 = 26 entonces m = 26 – 26 de donde m = 0
5) t + 54 = -3 entonces t = -3 – 54 de donde t = -57
6) n – 46 = 46 entonces n = 46 + 46 de donde n = 0
7) y – 58 = 58 entonces y = 58 + 58 de donde y = 116
8) y + 39 = 6 entonces y = -6 – 39 de donde y = – 45
9) 2h + 14 = 0 entonces 2h = -14 de donde h = -14/2, por lo tanto, h = -7
10) n/3 – 9 = 4 entonces 5n = 4 + 9 de donde n = (13)(3), por lo tanto, n = 39


Respuestas del ejercicio anterior.
Resolver ecuaciones con signos.
1) 2m/7 + 8 =- 32 entonces 2m/7 = -32 – 8 de donde 2m = -40 x 7 luego, m = -280/2, por lo tanto, = – 140
2) x/11 + 9 = -69 entonces x/11 = – 69 – 9 de donde x = -78 x 11, por lo tanto, x = – 858
3) w/14 + 6 = -24 entonces w/14 = – 24 – 6 de donde w = – 30 x 14, por lo tanto, w = – 420
4) 3h/5 + 10 = -50 entonces 3h/5 = – 50 – 10 de donde 3h = -60 x5 Por lo tanto, h = – 300/3, por lo tanto, h = – 100
5) -19x – 15 =- 19 entonces -19x = -19 + 15 de donde x = – 4/ -19, por lo tanto, x = 4 /19
6) 7k/4 – 18 = -74 entonces 7k/4 = -74 +18 de donde 7k = -56 x 4, luego, k = – 224/7, por lo tanto, k =-32
7) (4)(3) w = 72 entonces 12w = 72 de donde w = 72/12, por lo tanto,w = 6
8) (2)(3) h/5 = 30 entonces 6h/5 = 30 de donde 6h = 30 x 5, luego,
h = 150/6, por lo tanto, h = 25
9) 3/5x – 7 = 25 entonces 3/5 x = 25 + 7 de donde x = 32 x 5 /3, luego, x = 160/3, por lo tanto, x = 53.33
10) 4/7 y + 18 = 60 entonces 4/7 y = 60 – 18 de donde y = 42 x 7/4, luego, y = 294/4, por lo tanto, y = 73.5



Respuestas del ejercicio anterior.
Resolver las siguientes ecuaciones de primer grado.
1) En este caso, aplicamos las operaciones inversas y tomamos encuenta la ley de los signos, o sea, -5m = 30 – 10 donde -5m = 20 entonces m = 20 / -5 por lo que m = – 4
2) En este caso, aplicamos las operaciones inversas y tomamos encuenta la ley de los signos, o sea, 3x / -4 = 42 – 8 donde 3x = 34 x – 4 entonces x = -136 / 3 por lo que x = – 45.33
3) En este caso, primero multiplicamos el (-5) por cada uno de los términos que están dentro del paréntesis, después, aplicamos las operaciones inversas y tomamos encuenta la ley de los signos, o sea, -10x + 30 = – 16 donde -10x = – 16 – 30 entonces x = -46 / -10 por lo que x = 4.6
4) En este caso, primero multiplicamos el (6) por cada uno de los términos que están dentro del paréntesis, después, aplicamos las operaciones inversas y tomamos encuenta la ley de los signos, o sea, 6x – 18 + 20 = 75 donde 6x = 75 + 18 – 20 entonces x = 73 / 6 por lo que x = 12.16
5) En este caso, aplicamos las operaciones inversas y tomamos encuenta la ley de los signos, o sea, 4y – 10 = – 30 x 2 donde 4y = – 60 + 10 entonces y = – 50 / 4 por lo que y = -12.5
6) En este caso, primero multiplicamos el (-12) por cada uno de los términos que están dentro del paréntesis, después, aplicamos las operaciones inversas y tomamos encuenta la ley de los signos, o sea, -12z – 48 + 27 = 110 donde -12z = 110 + 49 – 27 entonces z = 131 / – 12 por lo que z = – 10.91
7) En este caso, primero multiplicamos el 5 (6) después, aplicamos las operaciones inversas y tomamos encuenta la ley de los signos, o sea, 5s + 30 = 200 donde 5s = 200 – 30 entonces s = 170 / 5 por lo que z = 34
8) En este caso, primero multiplicamos el (-6) por cada uno de los términos que están dentro del paréntesis, después, aplicamos las operaciones inversas y tomamos encuenta la ley de los signos, o sea, -18y + 48 – 26 = 25 x – 4 donde -18y = -100 – 48 + 26 entonces y = – 122 / -18 por lo que y = 6.77
9) ) En este caso, primero multiplicamos el (5) por cada uno de los términos que están dentro del paréntesis, después, aplicamos las operaciones inversas y tomamos encuenta la ley de los signos, o sea, 8x – 24 + 5x – 15 = 125 donde 13x = 125 + 24 + 15 entonces x = 164 / 13 por lo que y = 12.61
10) ) En este caso, primero multiplicamos el (4) y el (3)por cada uno de los términos que están dentro del paréntesis, después, aplicamos las operaciones inversas y tomamos encuenta la ley de los signos, o sea 20y – 48 – 6y – 21 = 280 donde 14y = 280 + 48 + 21 entonces y = 349 / 14 por lo que y = 24.92



Respuestas del ejercicio anterior.
Resolver ecuaciones con variables en ambos lados del signo de igualdad.
1) 9x = 44 – 2x entonces 9x + 2x = 44 de donde 11x = 44 luego, x = 44/11, por lo tanto, = 4
2) 5c = 28 + c entonces 5c c = 28 de donde 4c = 28, luego c = 28/4
Por lo tanto, c = 7
3) 2d = 36 + 5d entonces 2d – 5d = 36 de donde 3d = 36, luego d = 36/ 3, por lo tanto, d = 12
4) 4y + 20 = 5y + 9 entonces 4y – 5y = 9 – 20 de donde y = 11, luego y = 11/ 1, por lo tanto, y = 11
5) 9x – 3 = 2x + 46 entonces 9x – 2x = 46 + 3 de donde 7x = 49, luego, x = 49/7, por lo tanto, x = 7
6) c + 20 = 55 – 4c entonces c + 4c = 55 – 20 de donde 5c = 35, luego, c = 35/5, por lo tanto, c = 7
7) 6d – 12 – d = 9d + 53 + d entonces 5d 10d = 53 + 12 de donde 5d = 65, luego d = 65/ 5, por lo tanto, d = 13
8) 4x – 3 = 47 – x entonces 4x + x = 47 + 3 de donde 5x = 50, luego x = 40/5, por lo tanto, x = 10
9) 3m – 5m – 12 = 7m – 88 – 5 entonces 2m – 7m = 93 + 12 de donde 9m = 81, luego m = 81 / 9, por lo tanto, m = 9
10) 7x – 4 = 5x – x + 35 entonces 7x – 4x = 35 + 4 de donde 3x = 39
luego x = 39/3, por lo tanto, x = 13

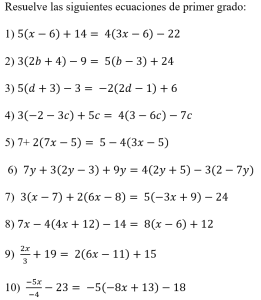
Respuestas del ejercicio anterior.
Resuelve las siguientes ecuaciones de primer grado.
1) 5 ( x – 6) + 14 = 4 ( 3 x – 6) – 22 en ste caso resolvemos las operaciones indicada y luego aplicamos las operaciones inversas, o sea, multiplicamos el 5 y 4 por cada uno de los términos que están dentro del parentecis, por lo que, 5x – 30 + 14 = 12x – 24 – 22 ahora, reunimos todas las variables de un lado del signo de igualdad y del otro lado del signo de igualdad todos los números, simpre aplicando las operaciones inversas, por lo que, 5x – 12x = -24 – 22 – 14 + 30 donde reducimos losterminos semejantes y tenemos – 7x = – 30 luego x = – 30 / – 7 por lo tanto x = 4.2
2) 3 ( 2 b + 4) – 9 = 5 ( b – 3) + 24 en ste caso resolvemos las operaciones indicada y luego aplicamos las operaciones inversas, o sea, multiplicamos el 3 y 5 por cada uno de los términos que están dentro del parentecis, por lo que, 6b + 12 – 9 = 5b – 15 + 24 ahora, reunimos todas las variables de un lado del signo de igualdad y del otro lado del signo de igualdad todos los números, simpre aplicando las operaciones inversas, por lo que, 6b – 5b = – 15 + 24 – 12 + 9 donde reducimos losterminos semejantes y tenemos b = 6
3) 5 ( d + 3) – 10 = – 2 ( 2 d – 1) + 6 en ste caso resolvemos las operaciones indicada y luego aplicamos las operaciones inversas, o sea, multiplicamos el 5 y -2 por cada uno de los términos que están dentro del parentecis, por lo que, 5d + 15 – 10 = – 4d + 2 + 6 ahora, reunimos todas las variables de un lado del signo de igualdad y del otro lado del signo de igualdad todos los números, simpre aplicando las operaciones inversas, por lo que, 5d + 4d = 2 + 6 – 15 + 10 donde reducimos losterminos semejantes y tenemos 9d = 3 luego d = 3 / 9 por lo tanto, simplificando d = 1 /3
4) 3 ( – 2 – 3 c) + 5 c = 4 ( 3 – 6 c) – 7 c en ste caso resolvemos las operaciones indicada y luego aplicamos las operaciones inversas, o sea, multiplicamos el 3 y 4 por cada uno de los términos que están dentro del parentecis, por lo que, -6 – 9c + 5c = 12 – 24c – 7c ahora, reunimos todas las variables de un lado del signo de igualdad y del otro lado del signo de igualdad todos los números, simpre aplicando las operaciones inversas, por lo que, – 9c + 5c + 24c + 7c = 12 + 6 donde reducimos losterminos semejantes y tenemos 16c = 18 luego c = 18 / 16 por lo tanto c = 1.12
5) 7 + 2 ( 7 x – 5) = 5 – 4 ( 3 x – 5) en ste caso resolvemos las operaciones indicada y luego aplicamos las operaciones inversas, o sea, multiplicamos el 2 y -4por cada uno de los términos que están dentro del parentecis, por lo que, 7 + 14x – 10 = 5 -12x + 20 ahora, reunimos todas las variables de un lado del signo de igualdad y del otro lado del signo de igualdad todos los números, simpre aplicando las operaciones inversas, por lo que, 14x + 12x = 5 + 20 + 10 – 7 donde reducimos losterminos semejantes y tenemos 26x = 28 luego x = 28 / 26 por lo tanto x = 1.07
6) 7 y + 3 ( 2 y – 3) + 9 y = 4 ( 2 y + 5) – 3 ( 2 – 7 y) en ste caso resolvemos las operaciones indicada y luego aplicamos las operaciones inversas, o sea, multiplicamos el 3, 4 y -3 por cada uno de los términos que están dentro del parentecis, por lo que, 7y + 6y – 9 + 9y = 8y + 20 – 6 + 21y ahora, reunimos todas las variables de un lado del signo de igualdad y del otro lado del signo de igualdad todos los números, simpre aplicando las operaciones inversas, por lo que, 7y + 6y + 9y – 8y – 21y = 20 – 6 + 9 donde reducimos losterminos semejantes y tenemos – 7y = 23 luego y = 23 / – 7 por lo tanto y = 3.28
7) 3 ( x – 7) + 2 ( 6 x – 8) = 5 ( -3 x + 9) – 24 en ste caso resolvemos las operaciones indicada y luego aplicamos las operaciones inversas, o sea, multiplicamos el 3, 2 y 5 por cada uno de los términos que están dentro del parentecis, por lo que, 3x – 21 + 12x – 16 = – 15x + 45 – 24 ahora, reunimos todas las variables de un lado del signo de igualdad y del otro lado del signo de igualdad todos los números, simpre aplicando las operaciones inversas, por lo que, 3x + 12x + 15x = 45 – 24 + 21 + 16 donde reducimos losterminos semejantes y tenemos 30x = 58 luego x = 58 / 30 por lo tanto x = 1.93
8) 7 x – 4 ( 4 x + 12) – 14 = 8 ( x – 6) + 12 en ste caso resolvemos las operaciones indicada y luego aplicamos las operaciones inversas, o sea, multiplicamos el -4 y 8 por cada uno de los términos que están dentro del parentecis, por lo que, 7x – 16x – 48 – 14 = 8x – 48 + 12 ahora, reunimos todas las variables de un lado del signo de igualdad y del otro lado del signo de igualdad todos los números, simpre aplicando las operaciones inversas, por lo que, 7x – 16x – 8x = – 48 + 12 + 48 + 14 donde reducimos losterminos semejantes y tenemos – 17x = 26 luego x = 26 / -17 por lo tanto x = – 1.52
9) 2 x / 3 + 19 = 2 ( 6 x – 11) + 15 en ste caso resolvemos las operaciones indicada y luego aplicamos las operaciones inversas, o sea, multiplicamos el 2 por cada uno de los términos que están dentro del parentecis, por lo que, 2x / 3 + 19 = 12x – 22 ahora, reunimos todas las variables de un lado del signo de igualdad y del otro lado del signo de igualdad todos los números, simpre aplicando las operaciones inversas, por lo que, 2x / 3 – 12x = – 22 – 19 donde reducimos losterminos semejantes, pero como la primera parte es una fracción, aplicamos la regla para restar fracciones con diferentes denominadores y tenemos 2x / 3 – 12x = 2x – 36x / 3 = – 33x / 3 = – 41luego – 33x = – 41 x 3 por lo tanto -33x = -123 entonces x = – 123 / – 33 de tal forma que, x = 3.72
10) – 5 x / – 4 – 23 = – 5 ( – 8 x + 13) – 18 en ste caso resolvemos las operaciones indicada y luego aplicamos las operaciones inversas, o sea, multiplicamos el -5 por cada uno de los términos que están dentro del parentecis, por lo que, -5x / – 4 – 23 = 40x – 65 – 18 ahora, reunimos todas las variables de un lado del signo de igualdad y del otro lado del signo de igualdad todos los números, simpre aplicando las operaciones inversas, por lo que, -5x / -4 – 40x = -65 – 18 + 23 donde reducimos losterminos semejantes, pero como la primera parte es una fracción, aplicamos la regla para restar fracciones con diferentes denominadores y tenemos -5x / -4 – 40x = -5x + 160x / 4 por lo tanto 155x / -4 = -65 – 18 + 23 entonces 155x = – 160 x – 4 de tal forma que, x = 640 / 155 por lo que x = 4.12



Respuestas del ejercicio anterior.
1) En este caso los números los consecutivos son 25 y 24.
2) En este caso se transfoma la ecuación literal a la forma matemática, o sea, 2x / 4 = 16 despejando 2x = 16 x 4 entonces x = 64 / 2 por lo que x = 32
3) En este caso se transfoma la ecuación literal a la forma matemática, o sea, x + 2 + 3x = 26 entonces reduciendo lo términos semejantes 4x + 2 = 26 despejando 4x = 26 – 2 donde x = 24 / 4 por lo que x = 6 y a la vez el 6 es el número menor.
4) En este caso se transfoma la ecuación literal a la forma matemática, o sea, x + 2x = 15 entonces reduciendo lo términos semejantes 3x = 15 despejando x = 15 / 3 por lo que x = 5
5) En este caso se transfoma la ecuación literal a la forma matemática, o sea, x – 10 = x / 2 en éste problemas debemos despejar el 2 y pasará a multiplicar la expresión 2 ( x – 10 ) = x entonces resolvemos la ecuación que se forma y tenemos 2x – 20 = x de donde 2x – x = 20 por lo que x = 20
6) En este caso los números consecutivos son 25 y 26 entonces 3 x 26 + 25 = 103
7) En este caso se transfoma la ecuación literal a la forma matemática, o sea, x + 2x – 1 = 26 entonces reduciendo lo términos semejantes 3x = 26 + 1 despejando x = 27 / 3 por lo que x = 9 luego 2 x 9 = 18 y Guillermo tiene 9 – 1 = 8 años.
8) En este caso sustituimos los valores en la expresión, o sea, 4(4) – 3(8) / 2(4) por lo que 16 – 24 / 8 = – 1
9) En este caso se transfoma la ecuación literal a la forma matemática, o sea, 1/5 x + x = 78 entonces debemos sumar las fracciones primero y luego busco un denominador común entre los denominadores 1/5 x + x = x + 5 x / 5 de donde 6 x / 5 = 78 luego despejando la variable, queda que x = 78 x 5 / 6, por lo tanto x = 65
10) En este caso se transfoma la ecuación literal a la forma matemática, o sea, 5( x + 2 ) + 12 x = 78 de donde 5x + 10 + 12x = 78 entonces resolvemos la ecuación y tenemos que 17x = 78 – 10 luego despejando x = 68/17, por lo tanto, x = 4 por lo que, el boleto de niño cuesta $4.
Ejercicios (22)
Resuelve las siguientes ecuaciones de primer grado.
1) Si hay dos números concecutivos y la suma del número menor más el triple del número mayor es igual a 103. ¿Cuál es el número menor?
2) Nora tiene 4 años más que Diana, dentro de dos años, Nora tendrá el doble de la edad de Diana.¿Cuántos años tiene Nora ahora?
3) En una zapatería se vendieron 340 pares de zapatos en un solo día, si el número de pares de zapatos deportivos vendidos fue 4 pares más que el doble del números de pares de zapatos de vestir vendodidos. ¿Cuántos pares de zapatos deportivos se vendieron?
4) El tio de Erica tiene el triple de la edad que tiene ella, hace 4 años, el tio de Erica tenía 4 veces la edad que tiene ella. ¿Cuántos años tiene Erica?
5) María tiene $4.20 en 36 monedas, y éstas son de quartes y nickels. ¿Cuántas monedas de cada una tiene ella?
&

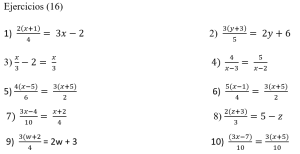
Respuestas del ejercicio anterior.
1) En este caso, debemos multiplicar en cruz y luego realizamos las operaciones indicadas, después aplicamos las operaciones inversas, o sea,
2(x + 1) = 4 (3x – 2) ahora, desarrollando 2x + 2 = 12x – 8 reunimos las variables y los números 2x – 12x = – 8 – 2 entonces -10x = – 10 despejando x = – 10 / – 10 por lo que x = 1
2) En este caso, debemos multiplicar en cruz y luego realizamos las operaciones indicadas, después aplicamos las operaciones inversas, o sea,
3(y + 3) = 5 (2y + 6) ahora, desarrollando 3y + 9 = 10y + 30 reunimos las variables y los números 3y – 10y = 30 – 9 entonces -7y = 21 despejando x = 21 / -7 por lo que x = – 3
3) En este caso, primero debemos resolver la resta de fracciones que hay de un lado de igualdad, o sea, x / 3 – 2 /1 = x – 6 / 3 ahora, tenemos que multiplicar en cruz y luego realizamos las operaciones indicadas, después aplicamos las operaciones inversas,
x – 6 / 3 = x /3 entonces 3(x – 6) = 3x desarrollando 3x – 18 = 3x reunimos las variables y los números 3x – 3x = 18 entonces 0 = 18 como la varible se hace cero, esto indica que la ecuación no tiene solucion.
4) En este caso, primero debemos resolver la resta de fracciones que hay de un lado de igualdad, o sea, x / 4 + 1 / 1 = x + 4 /4 ahora, tenemos que multiplicar en cruz y luego realizamos las operaciones indicadas, después aplicamos las operaciones inversas,
x + 4 / 4 = x / 4 entonces 4(x + 4) = 4x desarrollando 4x + 16 = 4x reunimos las variables y los números 4x – 4x = – 16 entonces 0 = 18 como la varible se hace cero, esto indica que la ecuación no tiene solucion.
5) En este caso, debemos multiplicar en cruz y luego realizamos las operaciones indicadas, después aplicamos las operaciones inversas, o sea,
2 x 4 (x – 5 ) = 6 x 3 (x + 5 ) ahora, desarrollando 8 (x – 5) = 18 (x + 5) seguimos desarrollando 8x – 40 = 18x + 90 reunimos las variables y los números 8x – 18x = 90 + 40 entonces -10x = 130 despejando x = 130 / – 10 por lo que x = -13
6) En este caso, debemos multiplicar en cruz y luego realizamos las operaciones indicadas, después aplicamos las operaciones inversas, o sea,
2 x 5 (x – 1 ) = 4 x 3 (x + 5 ) ahora, desarrollando 10 (x – 1) = 12 (x + 5) seguimos desarrollando 10x – 10 = 12x + 60 reunimos las variables y los números 10x – 12x = 60 + 10 entonces -2x = 70 despejando x = 70 / – 2 por lo que x = -35
7) En este caso, primero debemos resolver la resta de fracciones que hay de un lado de igualdad, o sea, 7x / 8 + 1 / 4 = 7x/ 8 + 1 (2) / 4 (8) luego 7x + 2 / 8 ahora, tenemos que multiplicar en cruz y luego realizamos las operaciones indicadas, después aplicamos las operaciones inversas, 7x + 2 / 8 = 3x /4 entonces 4(7x + 2) = 8(3x) desarrollando 28x + 8 = 24x reunimos las variables y los números 28x – 24x = 8 entonces 4x = 8 despejando x = 8 / 4 por lo que x = 2
8) En este caso, debemos multiplicar en cruz y luego realizamos las operaciones indicadas, después aplicamos las operaciones inversas, o sea,
2(z + 3) = 3(5 – z) ahora, desarrollando 2z + 6 = 15 – 3z reunimos las variables y los números 2z + 3z = 15 – 6 entonces 5z = 9 despejando z = 9 / 5 por lo que z = 1.8
9) En este caso, debemos multiplicar en cruz y luego realizamos las operaciones indicadas, después aplicamos las operaciones inversas, o sea,
2(x + 1) = 4 (3x – 2) ahora, desarrollando 2x + 2 = 12x – 8 reunimos las variables y los números 2x – 12x = – 8 – 2 entonces -10x = – 10 despejando x = – 10 / – 10 por lo que x = 1
10) En este caso, debemos multiplicar en cruz y luego realizamos las operaciones indicadas, después aplicamos las operaciones inversas, o sea,
10(3x – 7) = 10 x 3(x + 5) ahora, desarrollando 30x – 70 = 30x + 150 reunimos las variables y los números 30x – 30x = 150 + 70 entonces 0 = 220 como la varible se hace cero, esto indica que la ecuación no tiene solucion.













